现在大部分的MOSFET驱动电路均为电压源驱动。在MOSFET开启和关闭的过程中,依据栅极电压,沟道电流,漏极电压的变化,可细分为四个阶段,
- \(V_{GS}\)从零上升到\(V_{{GS}\_th}\) ,此时沟道电流和漏源电压没有任何变化。此段时间计为\(t_1\)
- \(V_{GS}\)从\(V_{{GS}\_th}\) 上升到\(V_{{GS}\_plateu}\) ,相应的,可以认为在这段时间内沟道电流从零上升到工作电流(感性负载?),而漏极电压保持不变。此段时间加上\(t_1\)计为\(t_2\)
- \(V_{GS}\)保持在\(V_{{GS}\_plateu}\) ,\(C_{GD}\)被充电,相应的,漏源电压从电源电压下降到\(V_{{DS}\_ON}\),而沟道电流近似不变。此段时间计为\(t_3\)
- \(V_{GS}\)从\(V_{{GS}\_plateu}\)上升到栅极驱动芯片输出电压,此为过驱动阶段。此阶段\(R_{{DS}\_ON}\)继续减小,\(V_{{DS}\_ON}\)有少许变化。
MOSFET关闭时,
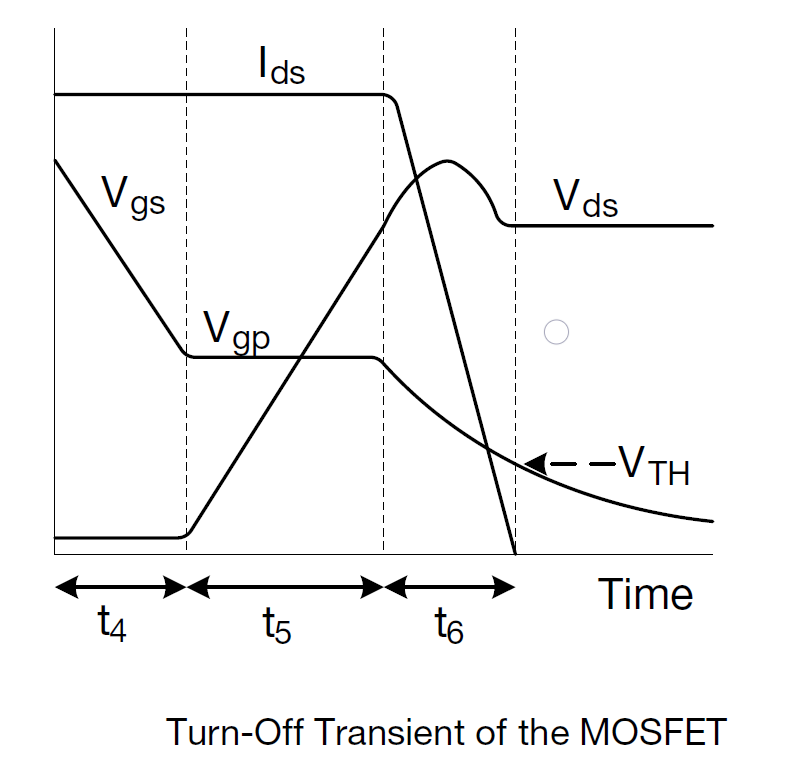
- \(V_{GS}\)从栅极驱动器输出电压下降到\(V_{{GS}\_plateu}\) ,此时沟道电流和漏源电压没有任何变化。此段时间计为\(t_4\)
- \(V_{GS}\)保持在\(V_{{GS}\_plateu}\) ,在这段时间内沟道电流保持不变,而漏源电压从\(V_{{DS}\_{ON}}\)上升到接近电源电压(感性负载?)。此段时间计为\(t_5\)
- \(V_{GS}\)从\(V_{{GS}\_plateu}\)下降到\(V_{{GS}\_th}\) ,沟道电流从工作电流迅速下降到零,快速的\(\frac{di}{dt}\) 导致\(V_{DS}\)出现上冲。此段时间计为\(t_6\)
- \(V_{GS}\)从\(V_{{GS}\_th}\) 下降到零,此过程对沟道电流和漏源电压没有任何影响,故一般不做研究
相应的波形如下所示,
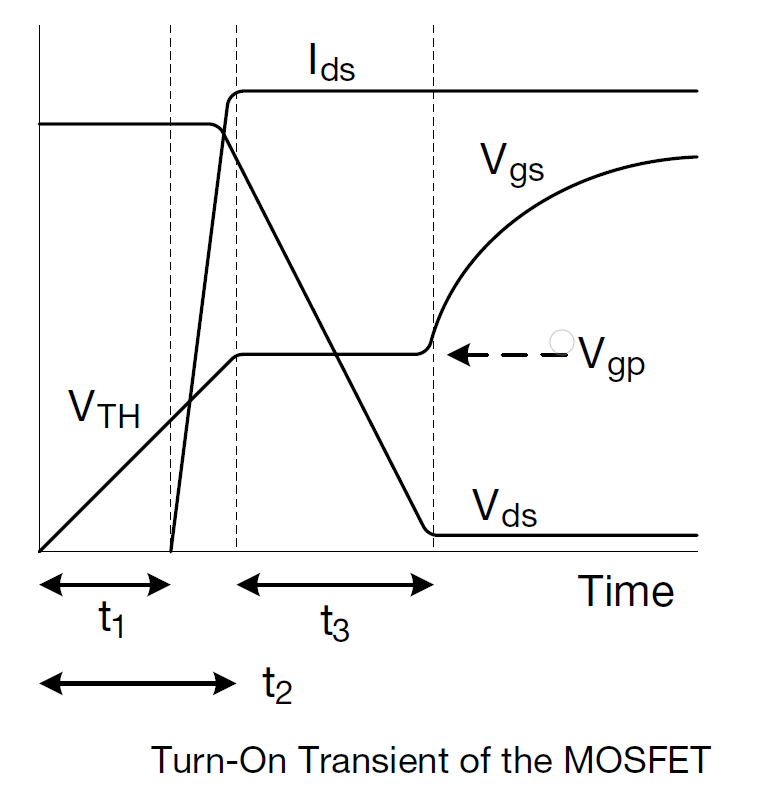
\(t_1\)以及\(t_2\)时间段由于\(V{_{DS}}\)不变,可等效为一阶RC电路充电过程,相应的时间计算如下,
\(t_1=R_GC_{iss}ln(\frac{1}{1-\frac{V_{GS\_TH}}{V_{GS}}})\)
\(t_2=R_GC_{iss}ln(\frac{1}{1-\frac{V_{GS\_plateu}}{V_{GS}}})\)
在\(t_3\)时间段,由于漏源电压的变化导致\(C_{GD}\)变化,其精确时间由\(Q_{GD}\)来计算,
\(t_3=R_G\frac{Q_{GD\_D}}{V_{DS\_D}}\frac{V_{DS}}{(V_{GS}-V_{GS\_plateu})}\)
简单估算则如下式给出,
\(t_3=R_GC_{GD}(\frac{V_{DS}}{V_{GS}-V_{{GS}\_plateu}})\)
同样的,各关断时间由以下式子给出,

上式里面\(t_5\)仅仅是简单的估算。准确值由下式给出,
\(t_5=R_G\frac{Q_{GD\_D}}{V_{DS\_D}}\frac{V_{DS}}{V_{GS\_}}\)
在芯片规格书中,一般用上升时间,下降时间,开启延迟等量来表示MOSFET的开关特性,它们和上述式子的关系如下,
\(t_{d\_on}=t_2\)
\(t_r=t_3\)
\(t_{d\_off}=t_4\)
\(t_f=t_5\)
由上面的分析不难看出,某一个开关管关闭到另一个开关管打开需要的最小时间间隔,也就是死区时间为,
\(T_{dead}=t_4+t_5+t_6-t_1\)
上面的式子仅仅考虑半桥MOSFET开关过程本身需要的最小死区时间。实际应用中,还要考虑驱动器的传播延迟失配时间\(t_{pd\_mismatch}\),输入PWM信号的skew,\(t_f\),\(t_r\)等影响因素。