噪声系数(noise figure, Harald T. Friis introduced in 1944)经常用来衡量低噪声放大器(LNA)或者输入级晶体管的噪声性能,其定义如下:
\(Noise Figure(NF) =10\lg{\frac{\frac{P_{si}}{P_{ni}}}{\frac{P_{so}}{P_{no}}}}\)
等于输入信噪比除以输出信噪比的对数,单位为dB,故而如果是功率比值,前面乘以系数10,如果是电压比值,乘以20
其实,最开始时候是噪声因子(noise factor)的概念 (Introduced in 1942 by Dwight O. North)
\(Noise Factor(N) =\frac{\frac{P_{si}}{P_{ni}}}{\frac{P_{so}}{P_{no}}}\)
热噪声,由于导体/导电媒介中载流子的不规则热运动导致的宏观电压波动,其值和绝对温度,测量带宽,和阻值相关
\(V_{no}=\sqrt{4KTRB}\)
\(K: Boltzmann\;Constant =1.38×10^{-23}\) K: 绝对温度(K) B:测量带宽(Hz)
在射频系统中,输入输出匹配通常以最大功率传输原则来设计,即后级的输入阻抗为前级输出阻抗的共轭复数,考虑纯电阻情形,则最大功率传输条件下,负载阻抗等于前级输出阻抗。满足此条件时,任意源电阻产生的热噪声电压在负载上的理论功率为
\(P=KTB\)
其值与源电阻阻值无关,而仅与绝对温度相关。故而,在相同带宽下,任意噪声源(或电路单元)可抽象出一个值:等效噪声温度。考察一个功率增益为A的待测单元,在接入匹配的输入电阻之后,在输出端测量其总噪声输出,输出包含两部分,一部分为源匹配电阻热噪声经电路放大后的输出,另一部分为待测单元产生的噪声。将输出噪声功率除以增益后,我们得到输入端的总等效噪声功率,将它带入电阻热噪声公式,可以得到一个温度T,它一般高于测量环境温度(通常为298K),其差值即为待测单元的等效噪声温度。
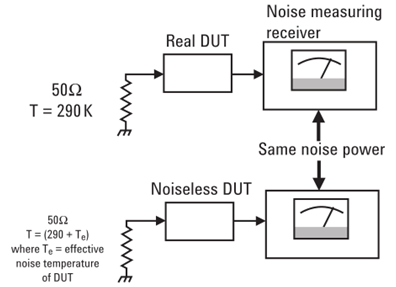
假设考察的放大器单元是一个线性系统,功率增益为A,则可以根据噪声系数的定义得到其另一种表达方式
\(NF=10\lg{\frac{\frac{P_{si}}{P_{ni}}}{\frac{P_{so}}{P_{no}}}}=10\lg{\frac{P_{no}P_{si}}{P_{ni}P_{Pso}}}=10\lg{(\frac{P_{no}}{AP_{ni}})}\)
即噪声系数表述为总输出噪声功率除以输入电阻热噪声和电路增益的乘积
噪声系数表征的局限性
1>增大输入匹配电阻的阻值,噪声系数计算值会下降,虽然输出总噪声增加了
2>噪声系数的定义对纯电抗性信号源无效
3>当电路本身贡献的噪声仅为信号源热噪声的一小部分时,计算电路的噪声系数或比较两个电路的噪声系数可能得到不精确的结果
4>在某一源阻抗下得到的噪声系数无法用来计算不同源阻抗下的电路噪声系数。因为源阻抗不同,则源电阻产生的噪声值不同,电路产生的噪声成分也有可能与源阻抗相关
运算放大器的噪声模型
同相和反向放大器的噪声模型如下(源自TI运放OPA1612 datasheet)
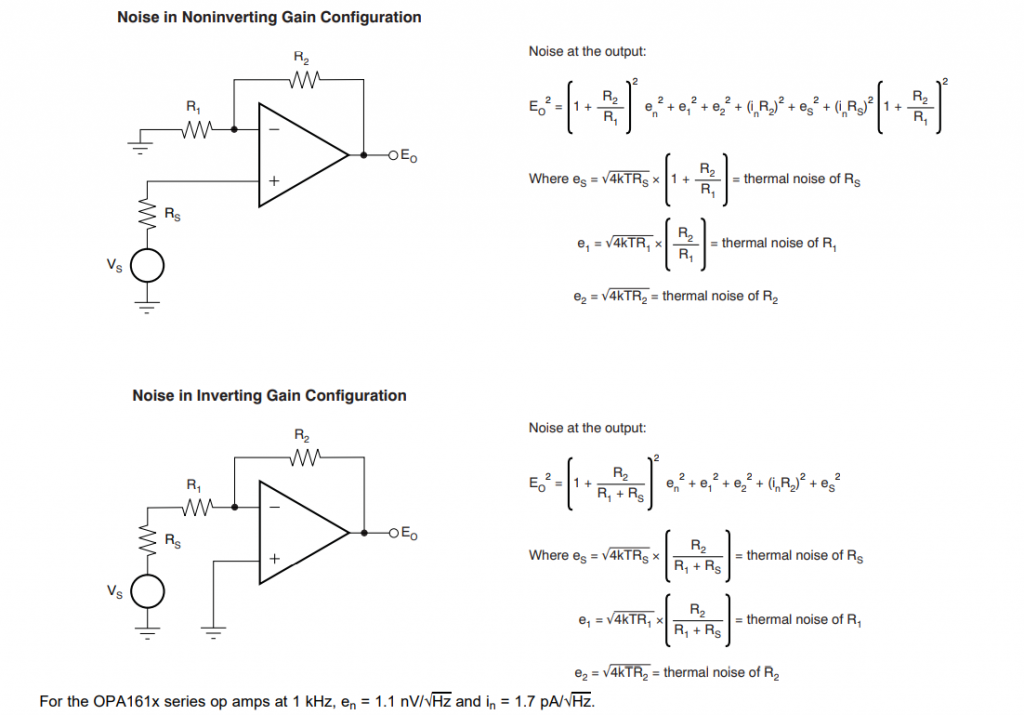
*作为对比,1Kohm电阻常温下的热噪声密度为\(e_n=4.07nV/\sqrt{\text{Hz}}\),100Ohm电阻的热噪声密度为\(e_n=1.29nV/\sqrt{\text{Hz}}\)
以反相放大器为例,放大倍数以\(\beta\)表示,我们有如下简化表达式,
\(E_o^2=(\beta+1)^2e_n^2+4KTR_2(\beta+1)+(i_nR_2)^2\)
考察一个放大倍数为10,100的放大器,反馈电阻R2假设为10K,运放分别选择为OPA1612,OPA827,带宽假设为20~20KHz(噪声密度数值选取1KHz值作为参考值),总输出噪声有效值分别为:
| 运放/放大倍数 | 1 | 10 | 100 |
| OPA1612 | 3.54uVrms | 6.72uVrms | 24.1uVrms |
| OPA827 | 2.81uVrms | 8.67uVrms | 60uVrms |
| LT1028 | 2.93uVrms | 6.32uVrms | 22uVrms |
依据上述噪声模型以及一些典型数据计算后有如下结论
1> 对于低阻信号源或者JFET输入型运放,低噪声运放的等效输入噪声电阻一般在数百欧姆以内,好的运放可以低至50Ohm以内
2> JFET输入运放的电流噪声成分远小于电压噪声,除非应用于输入阻抗极高或者放大倍数极高的电路,一般电流噪声成分可以忽略
晶体管噪声性能评估
和运放类似,晶体管等效噪声模型也由折合到输入端的电压和电流噪声源组成,故而晶体管的噪声系数由下述公式表示,
\(NF=10\lg{\frac{e_n^2+4KTR_s+(i_nR_s)^2}{4KTR_s}}\)
\(e_n\text{:= Noise Voltage of the Transistor referred to the input}\)
\(i_n\text{:= Noise Current of the Transistor referred to the input}\)
\(R_n\text{:= Source resistance}\)
由前述NF的另一种表述,可以看出,只要测量得到放大器单元输出端的总噪声功率(电压),以及放大器单元的增益,就可以根据源阻抗数值计算得出噪声系数。不过,要在极窄频带实现微小信号测量并非易事。通常,精确的测量晶体管的噪声系数曲线需要专业仪器才能实现。这里,我们用测量某一频带内晶体管输出总噪声的方法来评估晶体管的噪声性能
参考电路如下,
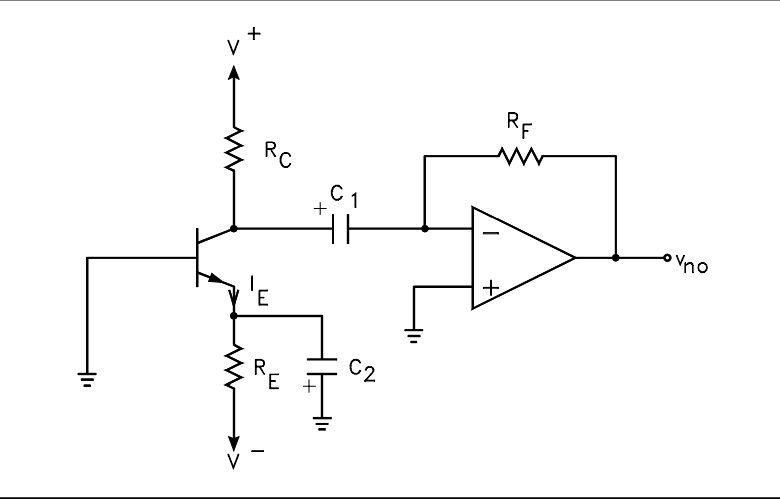
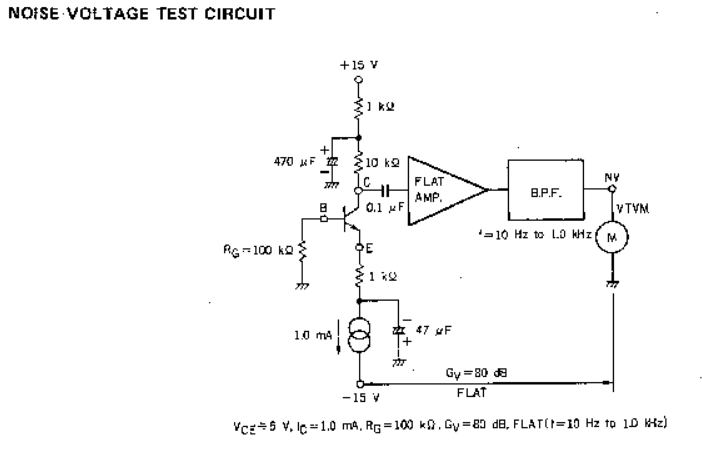
实际电路如下图所示,元器件的选择应该以最低噪声为目标。譬如电容选用钽电容,电阻选择vishay金属膜电阻,供电电源选择电池供电,整个测试设备放在多层屏蔽盒杜绝环境电磁波干扰。
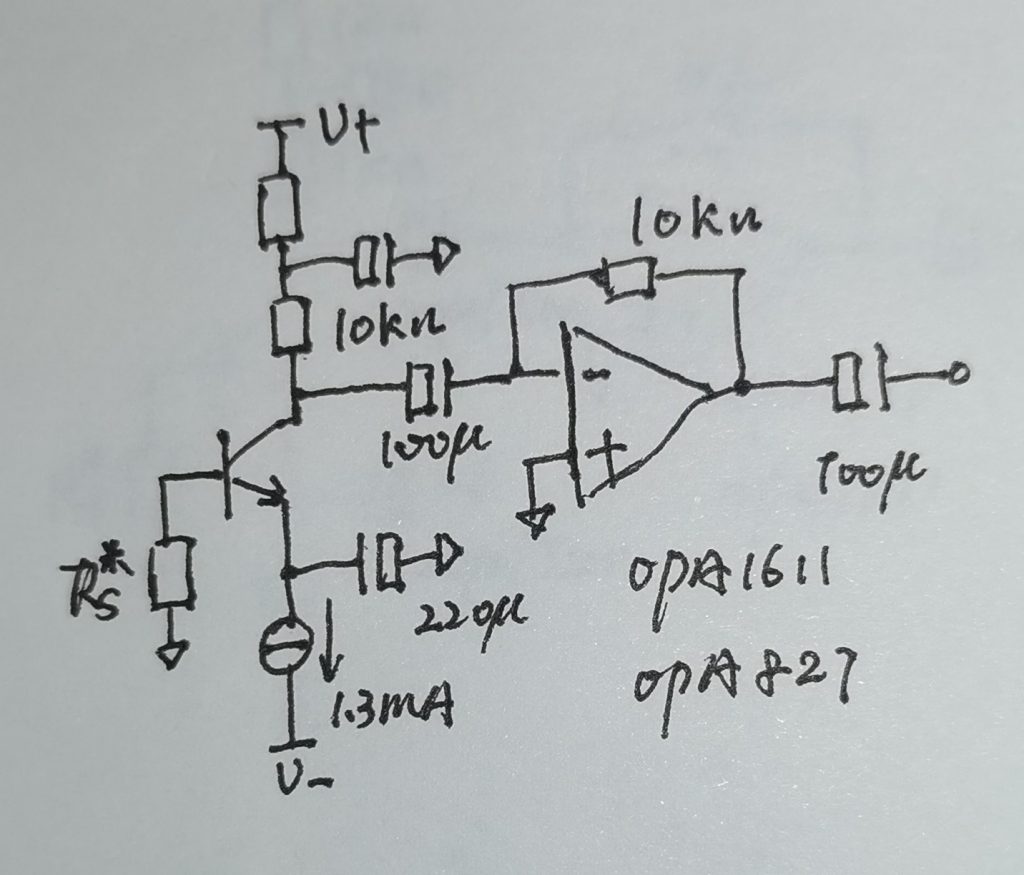
忽略晶体管输出端电阻的热噪声和运放的噪声分量之后,输出端测量得到的噪声为源电阻经放大之后的热噪声分量以及晶体管贡献的噪声分量。如果将晶体管的噪声等效到输入端,我们可以得到一等效输入噪声电压。其值的大小可以用来客观的评价晶体管在指定频带内的噪声性能。以晶体管基极为输入参考点,可以求得电路的电压增益为:\(g_m*R_f=\frac{I_c}{V_t}*R_f\),将\(R_E\)置换为恒流源即可得到确定的增益。令\(I_c=1.3mA\;,R_f=10\,K\,ohm\),则总电压增益为500。由前述运放噪声表达式不难看出,在\(R_f\)一定的情况下,运放电压增益越小,电阻贡献的总热噪声越小。
测试数据
用面包板搭建了一个简单测试电路,因为使用9V层叠电池供电的关系,Rc由10K改为2.2K,Rs设为332 Ohm,静态电流设置为1mA。室温下,如果假设待测BJT的输入阻抗远大于332 Ohm,则当带宽限制为22Khz的时候,输出端总噪声由电阻贡献的分量约为133uVrms。挑选了几款音频用三极管,实际测试结果如下,
| DUT型号 | 2SC2240GR(白字) | 2SC2240GR(激光) | 2SC2240BL(激光) | KSC3200GR | 2SC2229 | 2SC2705 | MPSA42 | KSC1845 |
| 总输出噪声 | 180uVrms | 165uVrms | 185uVrms | 180uVrms | 165uVrms | 200uVrms | 145uVrms | 200uVrms |
*测试条件:室温(30C),AP525,带宽:10·22.4KHz,仪器底噪+运放底噪:~5uVrms
从上述噪声测试结果得出的一些可能的推论:
- 同一型号管子,放大倍数越大,噪声越大。可能的原因是,在晶体管版图结构,制作工艺一致的前提下,放大倍数大的管子,基区相对掺杂浓度较低,基区扩散电阻会稍大,故而噪声较高。
- 相同工艺下,耐压越高的管子,噪声越小。